Skip to main content

2579. Count Total Number of Colored Cells

Medium

Description​

There exists an infinitely large two-dimensional grid of uncolored unit cells. You are given a positive integer n, indicating that you must do the following routine for n minutes:

At the first minute, color any arbitrary unit cell blue. Every minute thereafter, color blue every uncolored cell that touches a blue cell. Below is a pictorial representation of the state of the grid after minutes 1, 2, and 3.

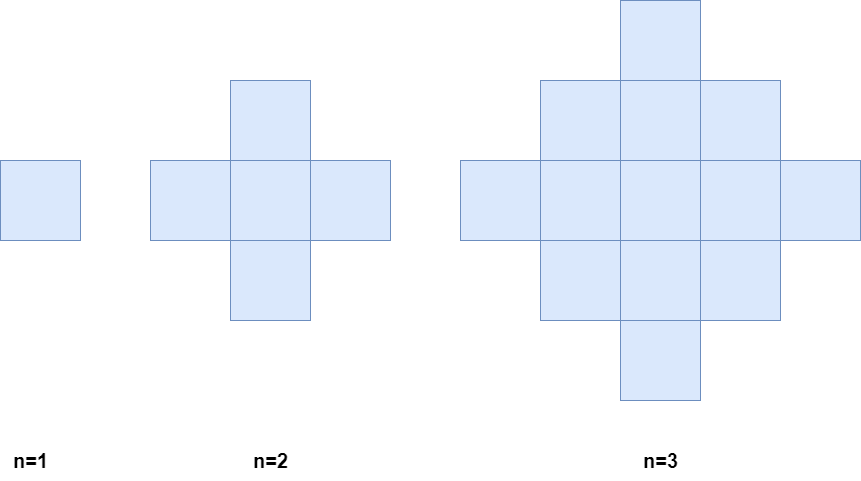
Return the number of colored cells at the end of n minutes.

Example 1:​

Input: n = 1
Output: 1
Explanation: After 1 minute, there is only 1 blue cell, so we return 1.

Example 2:​

Input: n = 2
Output: 5
Explanation: After 2 minutes, there are 4 colored cells on the boundary and 1 in the center, so we return 5.

Constraints:​

1 <= n <= 105

解題思路​

看了 Discussion 提到這題其實是個數學問題，套公式就能寫出時間複雜度空間複雜度皆為 O(1) 的完美答案
簡單整理了一下這公式的原理：

  1. 首先先觀察規律，當 n = 1 的時候 return 是 1 ，n 等於 2、3、4 的時候 return 分別會是 5、13、25
  2. 從上一點可以得知，每次 n + 1 的時候 return 的值會比前一個增加 4(n-1) ，如 13 = 5 + 4(3-1) = 5 + 8


不知道為啥會是 4 乘上 n-1 的可以看我剛剛畫的這張南部示意圖，加的 4(n-1) 就是角落顏色很醜的那幾塊，
n = 3 的情況就是 n=2 原本的中間五塊加上角落顏色很醜的那四部分 4(3-1)，也就是 5 + 4 * 2 = 13

  1. 可以根據上一點寫出一個累加的 function:　　
var coloredCells = function (n) {
  let answer = 1;
  for (let i = 0; i < n; i++) {
    answer += 4 * i;
  }
  return answer;
};

// 直接 4 * i 不需要 n-1 的原因是迴圈是從 0 開始的，第一個就是 0 也就是說本身就已經減 1 了
  1. 但還不夠完美，可以再更簡化。
    1. 每次 n + 1 的時候要加的值會比前一個增加 4(n-1) ，寫成算式就是 1 + 4*1 + 4*2 ... + 4(n-1)
    2. 且能簡化成1 + 4( 1 + 2 ... + (n-1))
    3. 而根據 1 + 2 + 3 + ... + m 的值是 (m * (m + 1)) / 2 的那個公式
    4. 將 n-1 代入公式的 m ，得出 1 + 4( 1 + 2 ... + (n-1)) 的值為(n-1) * (n-1 + 1) / 2 = (n-1) * n / 2
    5. 最後再回到每次 n + 1 的時候 return 的值會比前一個增加 4(n-1) 的地方並代入，會變成1 + 4 * ((n - 1) * n / 2)

所以原本的function可以改成這樣:

var coloredCells = function (n) {
  return 2 * n * (n - 1) + 1;
};

心得​

窩...數學好爛...